NHL WIN ODDS & PROJECTIONS

Every day, I simulate the NHL season 1M times in order to determine the probability of each outcome. During live games, I simulate each game 10K times on demand (i.e. whenever you load a live game page in /games). This article explains how these simulations work.

Model Overview

The model combines several key components to project game outcomes:

Offensive & Defensive Impact

I then used a prior-informed ridge regression (RAPM) to obtain a point estimate of the impact that each skater has on the rate at which their team generates and allows shots and expected goals for and against at even strength, shots and expected goals for on the power play, and shots and expected goals against on the penalty kill.

Shooting & Goaltending Impact

In order to obtain a point estimate of the impact that each skater has on the probability of their own shots becoming goals, and that each goaltender has on the probability of shots they face becoming goals, I followed a very similar process but instead used a non-prior informed (vanilla) ridge regression. This captures the individual shooting talent of skaters beyond what's explained by shot quality.

Multi-Year Forecasting

I repeated the regression process for every NHL season from 2007-2008 through 2024-2025. I then ran a linear regression on each of these seasons to obtain coefficient estimates that would provide me with the proper weights to place on years 1, 2, and 3 in order to most accurately forecast a player's performance in year 4, and then applied this to every NHL skater who played over each of the past 3 seasons.

Goaltender Projections

I initially planned on using the same process for goaltenders but found in testing on prior seasons that goaltender performance was not very repeatable from year-to-year, and that my projected goaltender performance played a much larger role in explaining variance in my projected standings than it did in the actual NHL standings.

This led me to "place less weight" on goaltending by repeating a similar process to the one I did with skaters but instead directly obtaining the fitted values from a linear regression, which pulled the projected performance of every goaltender much closer to zero. This improved the performance of the model in testing on prior seasons.

Converting Rates to Playing Time

Every projected value that I obtained came in the form of a rate; for the play-driving components the rate was per-minute, and for the shooting and saving components it was per-shot. Not all skaters will play the same number of minutes and not all skaters will take the same percentage of their team's shots when they are on the ice, which makes these numbers useless without an idea of how much they will play and shoot next season.

Ice Time Estimation

In order to estimate the number of minutes that each skater will play, I repeated the above process using every player's time-on-ice percentage (TOI%) in order to project their TOI% and then adjusted this percentage based on the projected TOI% of all of their teammates to determine a proper estimate of how much each player will actually play.

Shot Share Estimation

In order to estimate the percentage of their team's shots that each skater will take, I essentially repeated this process for shots and obtained an estimate of the percentage of their team's shots that each player will take. I then multiplied the percentage of their team's shots that I projected each shooter would take by the projected impact that each shooter has on their shots becoming goals.

Building Team Components

For each team, I use projected lineups directly from Daily Faceoff.

The Six Core Components

I summed up the projected impact on each component of the game for every player on each team. This summation provided me with a team's isolated impact on the following six components:

These six components make up the "guts" of the model.

Simulating Individual Games

To determine the rate at which each team would take shots and score goals on those shots, I merged the projected impact of each team with the corresponding impact of their opponent to determine the overall impact that each team would have on those components, and then added this to the league-average rate that teams take shots and score goals.

This process is repeated for the home and away team for every single game to obtain the rate at which they will take shots and score on the shots they take. Once these values are acquired, the simulation is ready to be run.

The Simulation Process

I start the simulation by creating a dataframe in R with 3,600 rows and 2 columns. Each row represents a second of the game I'm simulating, and each column contains a random estimate of whether a team will take a shot or not based on the rate at which they shoot; there is one column for each team's shots.

If a team does take a shot, I estimate whether that shot will become a goal based on the rate at which they score on their shots. Once this process is complete for every row, the number of goals scored by each team is summed and if one team has scored more, a winner is declared.

Model Validation

When initially building the model, I tested the model on the 2019–2020 season following the same process and used log loss and average error between projected standings points per 82 games and actual standings points per 82 games.

The test was slightly different from a true and proper test; I was simultaneously at an unfair advantage because I had access to the first team that a player played for and an unfair disadvantage because I was not updating lineups every game. I take my results with a grain of salt due to this, but still feel confident based on the results that the model performs well.

Historical Model Results

The model was deployed starting in the 2020–2021 season and performed quite well against other public models. During the 2021 Stanley Cup Playoffs, the model finished with the lowest log loss among all tracked models, correctly giving the Tampa Bay Lightning the highest probability of winning the Cup.

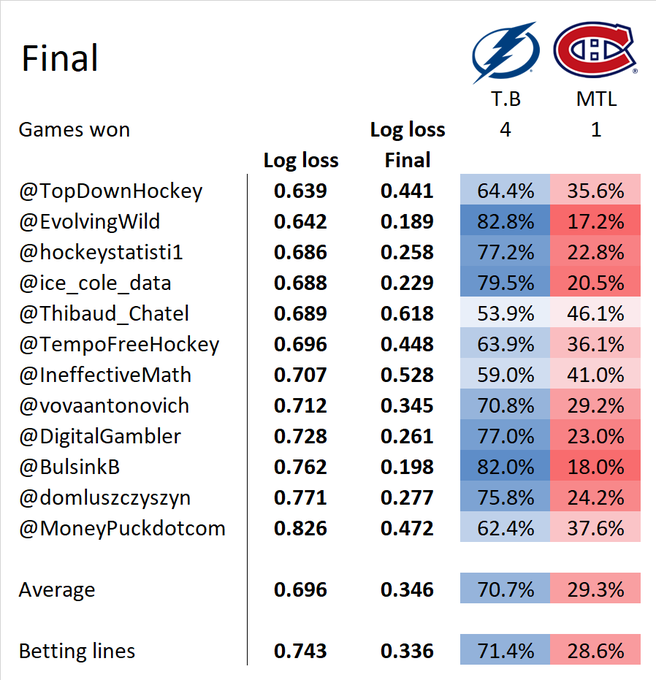
2021 Playoffs: Model comparison by log loss — tracked by @HockeySkytte on Twitter.

Playoff Odds & Standings Projections

Using the same game simulation model described above, each day I simulate the remainder of the NHL regular season, along with the entirety of the Stanley Cup Playoffs (based on my simulated regular season) 1 million times.

The probabilities which I report — such as Make Playoff Probability, Stanley Cup Probability, etc. for each team — are the empirical frequencies at which these outcomes are observed across all simulations. The projected points are the mean point totals per team across all of the 1M simulations.